
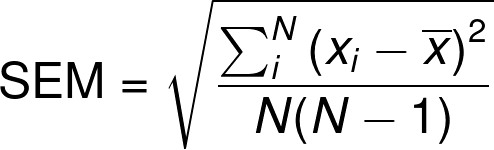

To calculate the standard error of any particular sampling distribution of sample- mean differences, enter the mean and standard deviation (sd) of the source population, along with the values of n a and n b, and then click the "Calculate" button.ĭistribution standard error of sample-mean differences = ± sd of source

Where sd 2 = the variance of the source population (i.e., the square of the standard deviation) The difference between the means of two samples, A and B, both randomly drawn from the same normally distributed source population, belongs to a normally distributed sampling distribution whose overall mean is equal to zero and whose standard deviation ("standard error") is equal to square.root Images not copyright InfluentialPoints credit their source on web-pages attached via hypertext links from those images.The logic and computational details of this The 5 cm can be thought of as a measure of the average of each individual plant height from the mean of the plant. We can say that our sample has a mean height of 10 cm and a standard deviation of 5 cm. Step 2: Calculate each measurements deviation from the mean (Mean minus the individual measurement). 1, Equations 1 and 2).In such models, approximately 68. Standard Error Calculation 9/22/04 STANDARD ERROR CALCULATION Procedure: Step 1: Calculate the mean (Total of all samples divided by the number of samples). In other words, a normally distributed statistical model can be achieved by examining the mean and the SD of the data (Fig. Let’s say we have a sample of 10 plant heights. As mentioned previously, using the SD concurrently with the mean can more accurately estimate the variation in a normally distributed data. In good agreement with both the (approximate) formula above - and with the estimated standard error for such a mean (using σ x/√n).įollowing an identical procedure, sampling a slightly skewed population, the standard deviation of their medians was only 1.19698 times the standard deviation - and when we sampled a highly skewed population, the standard deviation of their medians dropped to just 1/ 10 18 of the standard deviation of their means.Įxcept where otherwise specified, all text and images on this page are copyright InfluentialPoints, all rights reserved. The standard deviation is a measure of the variability of a single sample of observations. Imagine that you start a study but then increase the sample size. The denominator is the square root of the sample size (N), which is an adjustment for the amount of data. The numerator () is the sample standard deviation, which represents the variability present in the data. Repeating this calculation 5000 times, we found the standard deviation of their 5000 medians (0.40645) was 1.25404 times the standard deviation of their means. Here’s the equation for the standard error of the mean. square. Since the median is usually only used when the data are not drawn from a normally distributed population, this rather limits the usefulness of this formula, and it is rarely used.įor example, using R, it is simple enough to calculate the mean and median of 1000 observations selected at random from a normal population (μ x=0.1 & σ x=10). The difference between the means of two samples, A and B, both randomly drawn from the same normally distributed source population, belongs to a normally distributed sampling distribution whose overall mean is equal to zero and whose standard deviation ('standard error') is equal to. the sample is drawn from a normally distributed population.
#HOW TO CALCULATE STANDARD ERROR OF THE MEA HOW TO#
Learn how to calculate standard deviation of mean with.

Sample size 2 - Sample size 2 is the size of the sample population 2. Standard deviation 2 - Standard deviation 2 is the standard deviation of sample 2. Sample Size 1 - Sample Size 1 is the size of the 1st Sample Population. SE (median) is the standard error of the median, Standard Deviation - The Standard Deviation is a measure of how spread out numbers are.Providing certain assumptions are made, the standard error of the median can be estimated by multiplying the standard error of the mean by a constant:


 0 kommentar(er)
0 kommentar(er)
